在深度学习中,数值表示是一个常常被忽略的内容,可能从事模型量化领域的研究人员会有所了解,但是大部分的研究人员都对其了解甚少。但是一个设计合理的数值格式能够更好地加速模型训练和推理,在深度学习的工业化和实际落地中是非常重要的。近年来,为了加速深度学习,进一步挖掘硬件的性能,业界发明了一些新的数值格式,如本文中所介绍的TF32和BF16格式。其主要思想是利用深度学习对表示范围敏感而对精度不敏感这一特性,重新设计浮点数的表示,达到了一个更加好的平衡。
1. 单精度浮点数格式FP32(背景知识)
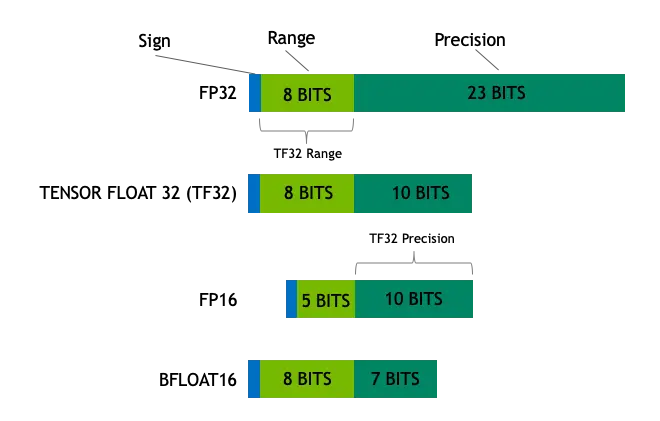
在深度学习中,单精度浮点数格式 FP32 是一种广泛使用的数据格式,其可以表示很大的实数范围,足够深度学习训练和推理中使用。这种格式使用4个 bytes(32bits)表示,其示意图如下。这 32 bits共分为3个部分:
- 第一部分为符号位 s,占 1 bit,用来表示正负号;
- 第二部分为指数偏移值 k,占 8 bits,用来表示其是2的多少次幂;
- 第三部分是分数值 M,占 23 bits,用来表示该浮点数的数值大小。
基于上述表示,浮点数的值可以用以下公式计算:(-1)^s×M×2^k
上述公式隐藏了一些细节,如指数偏移值 k 使用的时候需要加上一个固定的偏移值,但是这些与本文的主题无关,因此不再赘述了。
根据上述公式,我们可以计算其可以表示的实数范围为 1.18×10^(-38) 至 3.4×10^(38)。另外我们还可以得出一些结论,指数偏移值可以决定浮点数的表示范围,而分数值决定浮点数的有效数字位数。
2. Tensor Float 32 格式
Tensor Float 32 是 Tensor Core 支持新的数值类型,从 NVIDIA A100 中开始支持。A100 的普通 FP32 的峰值计算速度为 19.5 TOPs,而TF32的峰值计算速度为 156 TOPs,提升了非常多。
在深度学习中,其实我们对浮点数的表示范围比较看重,而有效数字不是那么重要。在这个前提下,TF直接就把 FP32 中 23 个分数值截短为 10 bits,而指数位仍为 8 bits,总长度为 19 (=1 + 8 + 10) bits。至于为什么是 10 bits 就够了,那是因为 FP16 就只有 10 bits 用来表示分数值。而在实际测试中,FP16 的精度水平已经足够应对深度学习负载,只是表示的范围不够广而已。
借助 NVIDIA 开发的深度学习库,用户可以无感地使用 TF32 而无需任何额外的操作。底层库会自动地将 FP32 转换为 TF32 进行计算,并将结果在转换为 FP32。
3. Brain Float 16 格式
Brain Float 16 格式是 Google 在 TensorFlow 中引入的新数据类型,其可以认为是直接将 FP32 的前16位截取获得的(可以参考这里)。至于设计思路和上面的 TF32 是一样的,都是深度学习对表示范围敏感而对精度不敏感。但是 Google 更加暴力,直接将分数值砍到只剩下 7 bits。
这个格式现在被许多的硬件直接支持了,如最新的Intel CPU (Cooper Lake 及以上)、NVIDIA GPU (Ampere 及以上,如 A100)和 Google TPU v2/v3。